힙(heap)

힙(heap) : 데이터에서 최댓값과 최솟값을 빠르게 찾기 위해서 고안된 완전 이진 트리 형태의 자료구조

힙을 통해 우선순위큐를 효율적으로 구현할 수 있음

힙의 특징

완전 이진 트리 구조를 가짐
부모 노드와 자식 노드 간의 대소 관계가 성립함 (형제 노드 간 관계 없음)
최대 힙(Max Heap)과 최소 힙(Min Heap) 두 종류가 존재
최댓값 최솟값 조회의 시간 복잡도: O(1)
삽입/삭제 연산의 시간 복잡도: O(log n)

완전 이진 트리(Complete Binary Tree): 모든 레벨이 완전히 채워져 있으며, 마지막 레벨에서는 노드들이 가능한 가장 왼쪽부터 채워져 있는 이진 트리

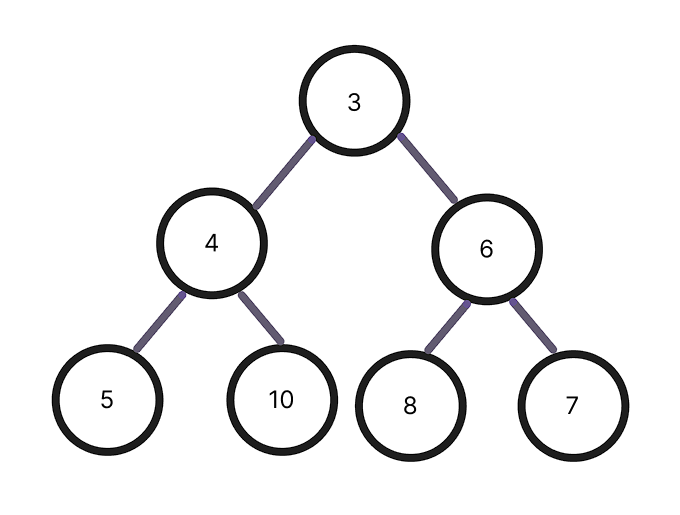
최대 힙: 루트 노드가 최댓값 → 부모 노드(key) ≥ 자식 노드(key)

최소 힙: 루트 노드가 최솟값 → 부모 노드(key) ≤ 자식 노드(key)

힙의 구현 방법

가장 일반적으로 배열을 이용하여 구현한다
- 우선순위큐 또한 배열로 구현된 heap으로 구현되어 있음
인덱스 계산을 통해 부모-자식 관계를 쉽게 표현할 수 있음
- 부모 노드의 인덱스: 자식 노드가 i 일 때 (i-1)/2
- 왼쪽 자식 노드: 부모 노드의 인덱스가 i일 때 2i + 1
- 오른쪽 자식 노드: 부모 노드의 인덱스가 i일 때 2i + 2
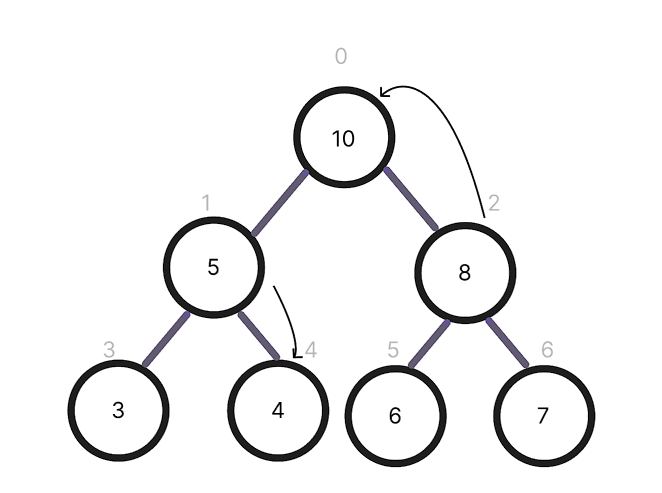
  - ex) 배열 [10, 5, 8, 3, 4, 6, 7] 로 표현된 힙이 존재할 때
  - i = 2 (value: 8)의 부모는 (2-1)/2 = 0 (value: 10)
  - i = 1 (value: 5)의 오른쪽 자식 노드는 2*1 + 2 = 4(value: 4)

힙의 삽입과 삭제 연산

두 연산의 시간 복잡도: O(log n)

삽입 연산
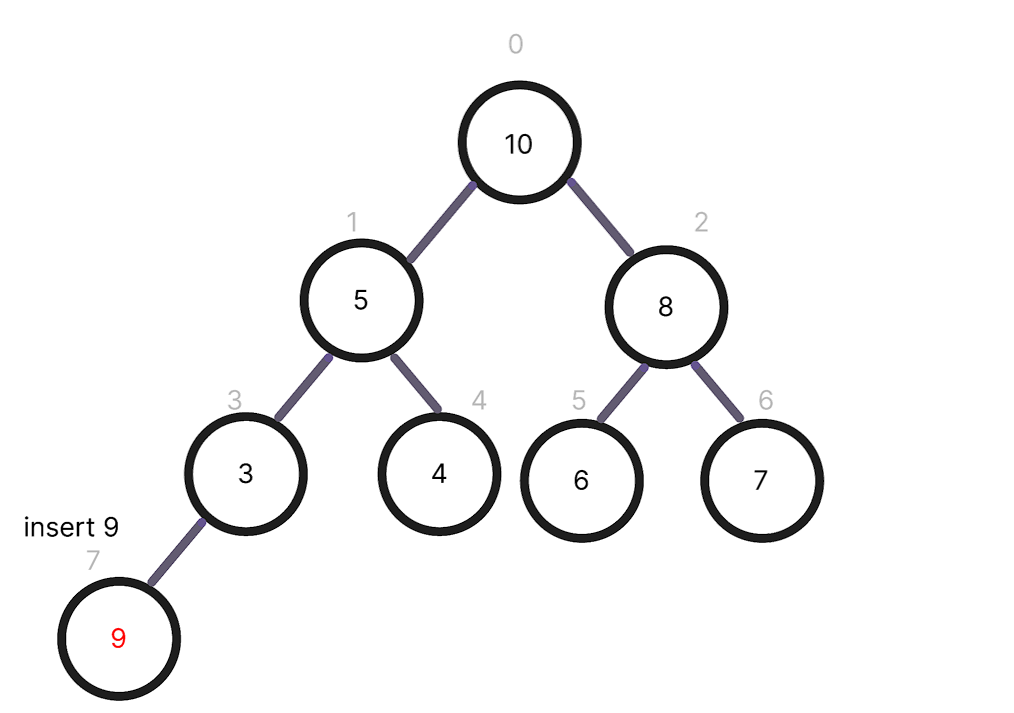
1. 새 노드를 트리의 마지막 위치에 추가한다
2. 부모 노드와 비교하여 힙의 조건을 만족할 때까지 위치를 교환한다 ( Heapify-up: 아래에서 위로 올라가며 정렬)

public void insert(int value) {
    heap.add(value);  // 힙의 끝에 새로운 값 추가
    int current = heap.size() - 1;

    while (current > 1 && heap.get(current) > heap.get(current / 2)) {  // 부모보다 크면 교환
        swap(current, current / 2);
        current = current / 2;
    }
}

최대 힙에서의 삽입 연산 과정

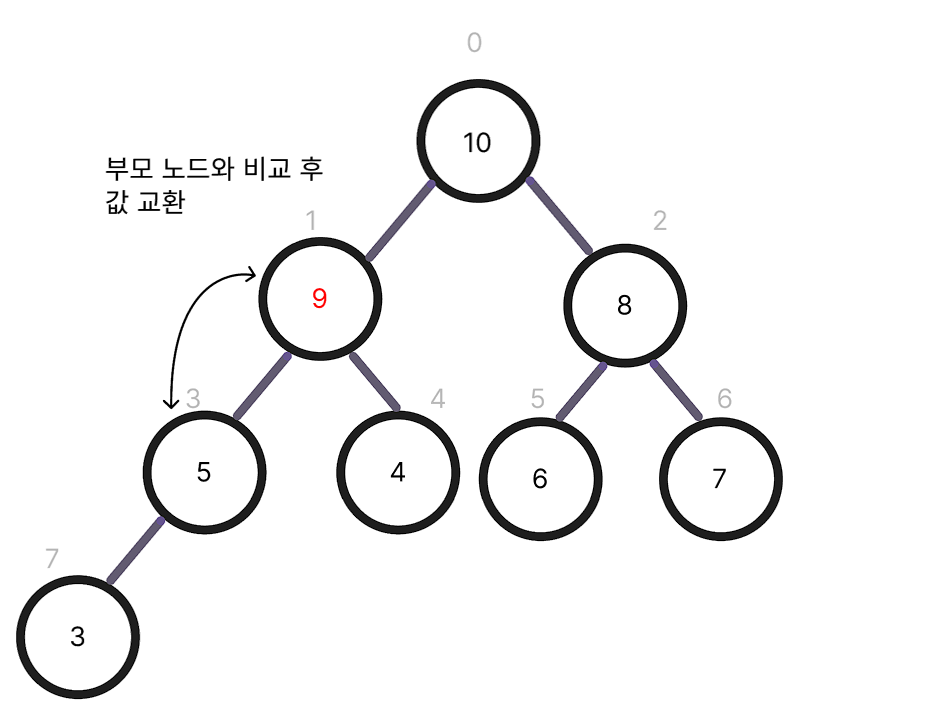
삭제 연산
1. 루트 노드를 삭제한다
2. 마지막 노드를 루트 위치로 이동시킨다
3. 자식 노드들과 비교하여 힙의 조건을 만족할 때까지 위치를 조정한다
  ( Heapify-down: 위에서 아래로 내려가며 정렬 )

// 삭제 메서드 (최댓값 삭제)
public int delete() {
    if (heap.size() <= 1) return -1;  // 힙이 비어있을 때 예외 처리
    int maxValue = heap.get(1);  // 루트 노드가 최댓값
    heap.set(1, heap.get(heap.size() - 1));  // 마지막 값을 루트로 이동
    heap.remove(heap.size() - 1);

    int current = 1; 
    while (true) { // 힙 속성을 만족할 때까지 아래로 내려가며 비교
        int leftChild = current * 2;
        int rightChild = current * 2 + 1;
        int maxIndex = current;  // 현재 노드와 자식 노드 중 가장 큰 값을 가진 노드의 인덱스
        
        // 왼쪽 자식 노드가 현재 노드보다 큰 경우
        if (leftChild < heap.size() && heap.get(maxIndex) < heap.get(leftChild)) {
            maxIndex = leftChild;
        }
        // 오른쪽 자식 노드가 현재 노드보다 큰 경우
        if (rightChild < heap.size() && heap.get(maxIndex) < heap.get(rightChild)) {
            maxIndex = rightChild;
        }
        if (maxIndex == current) break; //현재 노드가 자식들보다 크거나 같아서 내려갈 필요가 없음

        swap(current, maxIndex); // 현재 노드와 자식 노드 위치 교환
        current = maxIndex; // 현재 위치를 새 위치로 업데이트
    }
    return maxValue;
}

최대 힙에서의 삭제 연산 과정