이진탐색트리

이진탐색(Binary Search)

탐색에 소요되는 시간: O(log n)
삽입/삭제 불가

연결리스트(Linked List)

탐색에 소요되는 시간: O(n)
삽입/삭제에 소요되는 시간: O(1)

이진탐색트리(Binary Search Tree)

이진탐색(탐색) + 연결리스트(삽입/삭제)
탐색/삽입/삭제에 소요되는 시간
- 최적 및 평균: O(log n)
  - 트리의 높이에 비례
- 최악: O(n)
  - 치우친 트리의 경우
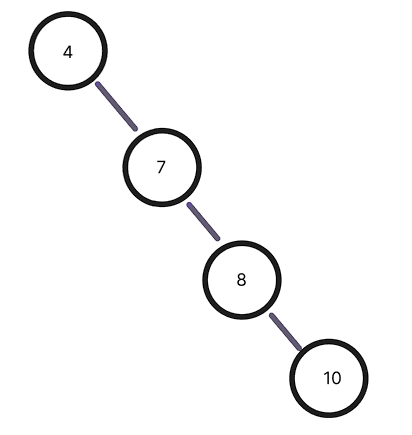
    치우친 트리
장점
- 검색, 삽입, 삭제 모두 평균적으로 O(log n) 성능
- 중위 순회시 정렬된 순서로 데이터 접근 가능
- 유연한 크기 조정 가능
단점
- 균형이 무너지면 성능이 O(n)까지 저하될 수 있음
  - 이진탐색트리의 단점인 불균형 문제를 해결하기 위해 자가균형 이진탐색트리(삽입/삭제 연산 시 트리를 재조정)를 사용할 수 있음
    - AVL Tree
    - Red-Black-Tree
- 중복 데이터 처리가 까다로움
- 추가 메모리 공간이 필요(포인터 저장)

이진탐색트리 만족 조건

각 노드의 왼쪽 서브트리에는 노드의 요소보다 작은 요소를 가진 노드로 구성
각 노드의 오른쪽 서브트리에는 노드의 요소보다 큰 요소를 가진 노드로 구성
각 서브트리는 각각의 이진탐색트리
각 노드의 자식이 2개 이하
중복된 요소는 허용하지 않음

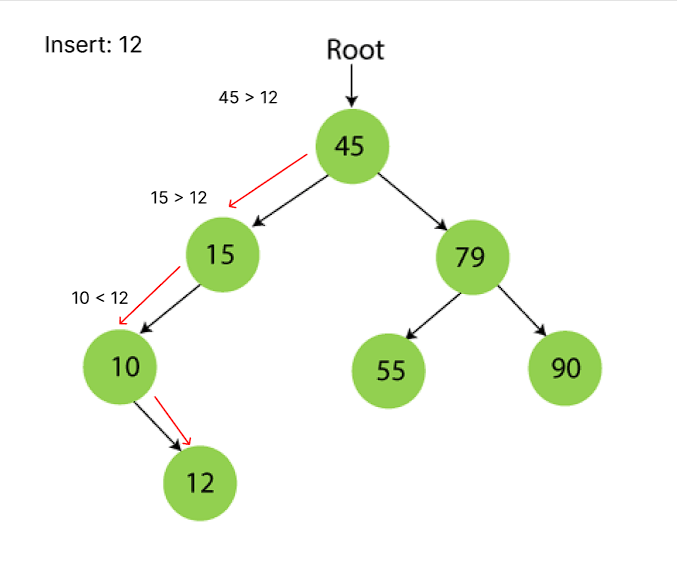
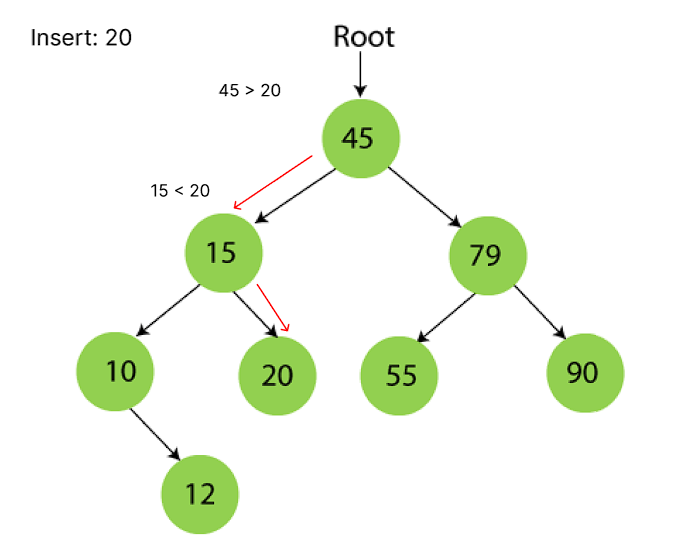
삽입 과정

루트 노드에서 시작
삽입할 값을 현재 노드와 비교
삽입할 값이 현재 노드보다 작으면 왼쪽 자식으로, 크면 오른쪽 자식으로 이동
2 - 3 반복

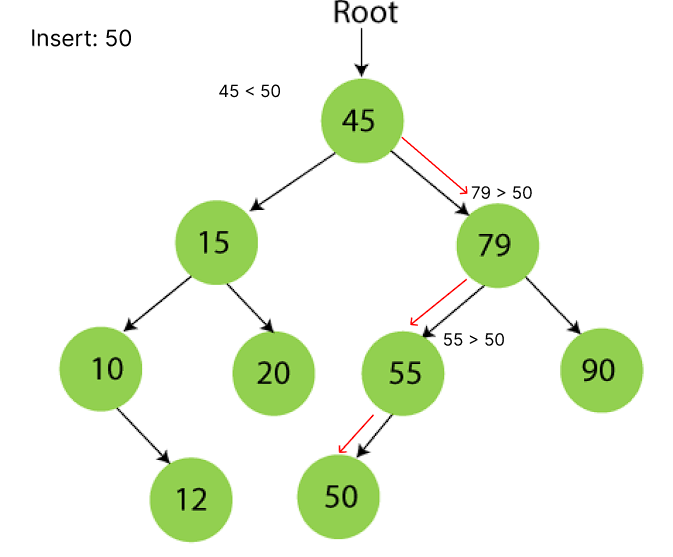
탐색 과정

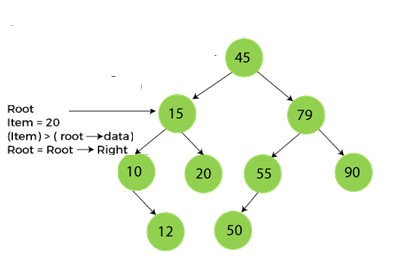
검색할 요소와 트리의 루트 요소를 비교
루트가 대상 요소와 일치하면 노드의 위치를 반환
일치하지 않으면 항목이 루트 요소보다 작은지 확인하고 루트 요소보다 작으면 왼쪽 하위 트리로 이동
루트 요소보다 크면 오른쪽 하위 트리로 이동
일치 항목을 찾을 때까지 위의 절차를 재귀적으로 반복
요소를 찾지 못하거나 트리에 존재하지 않으면 NULL을 반환

삭제 과정

삭제는 3가지 경우에 따라 다르게 연산된다

리프 노드일 때
- 부모 노드와의 연결 제거
자식을 하나만 갖고 있는 노드일 때
- 자식 노드와 삭제할 노드의 위치를 변경
- 삭제할 노드를 제거
- 노드를 지운 후 그 자식을 부모 노드와 연결해주는 과정과 동일
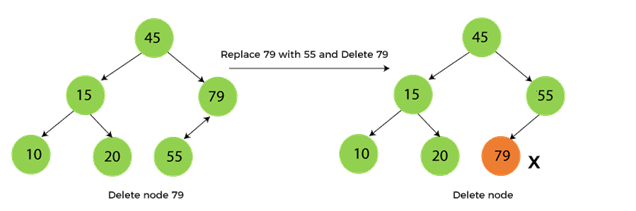
자식을 두개 갖고 있는 노드일 때
- 후속 노드(successor) 찾기
  - 삭제할 노드의 오른쪽 서브트리에서 가장 작은 값을 가진 노드
  - 오른쪽 자식으로 한 번 간 후, 계속 왼쪽 자식을 따라가면 됨
- 후속 노드의 값을 삭제할 노드의 위치로 복사
- 후속 노드를 삭제 (이때 후속 노드는 항상 자식이 최대 1개)

// 자식을 두 개 갖는 루트 노드(50)를 삭제하는 과정

1) 처음 상태:          2) 50을 60으로 대체:     3) 60 자리 삭제(자식이 하나인 노드 삭제):
     50                     60                      60
    /  \                   /  \                    /  \
   30   70       →       30   70        →        30   70
      /  \                  /  \                     /  \
     60   80              60   80                  65   80
      \                    \
      65                   65

출처

https://www.javatpoint.com/binary-search-tree

https://underdog11.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Binary-Search-Tree-%EC%9D%B4%EC%A7%84%ED%83%90%EC%83%89-%ED%8A%B8%EB%A6%AC-%EA%B8%B0%EB%B3%B8%EC%A0%95%EB%A6%AC-%EA%B5%AC%ED%98%84-%EA%B2%80%EC%83%89%EC%97%B0%EC%82%B0-%EC%82%AD%EC%A0%9C%EC%97%B0%EC%82%B0-Kotlin-%EA%B5%AC%ED%98%84

https://ratsgo.github.io/data%20structure&algorithm/2017/10/22/bst/