[level 3] 섬 연결하기 - 42861
성능 요약
메모리: 85.5 MB, 시간: 0.87 ms
구분
코딩테스트 연습 > 탐욕법(Greedy)
채점결과
정확성: 100.0
합계: 100.0 / 100.0
제출 일자
2024년 11월 13일 14:31:07
문제 설명
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한사항
- 섬의 개수 n은 1 이상 100 이하입니다.
- costs의 길이는
((n-1) * n) / 2이하입니다. - 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
- 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
- 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
- 연결할 수 없는 섬은 주어지지 않습니다.
입출력 예
| n | costs | return |
|---|---|---|
| 4 | [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] | 4 |
입출력 예 설명
costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.

해당 문제는 최소 신장 트리(MST) 유형으로 크루스칼 알고리즘을 활용하여 해결할 수 있다
그래프 내의 모든 정점들을 가장 적은 비용으로 연결하기 위해 사용됨


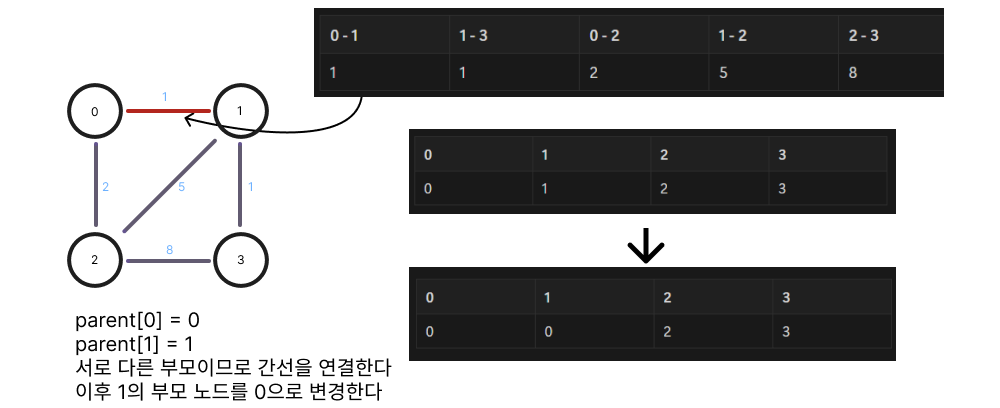
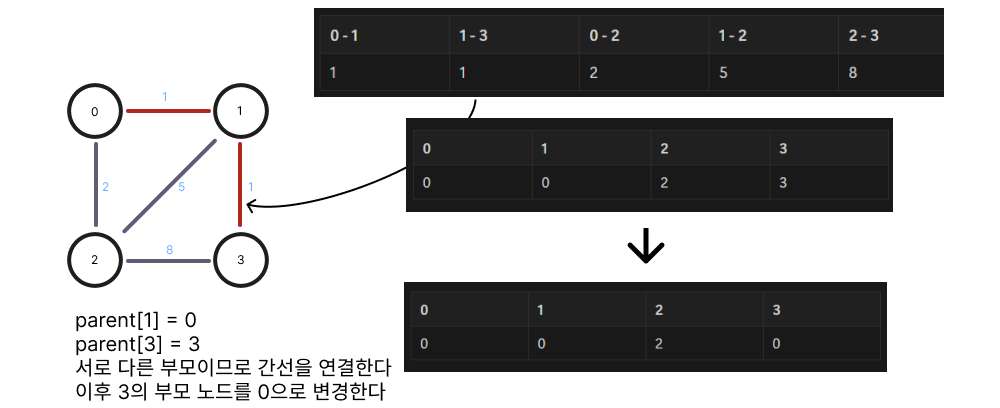
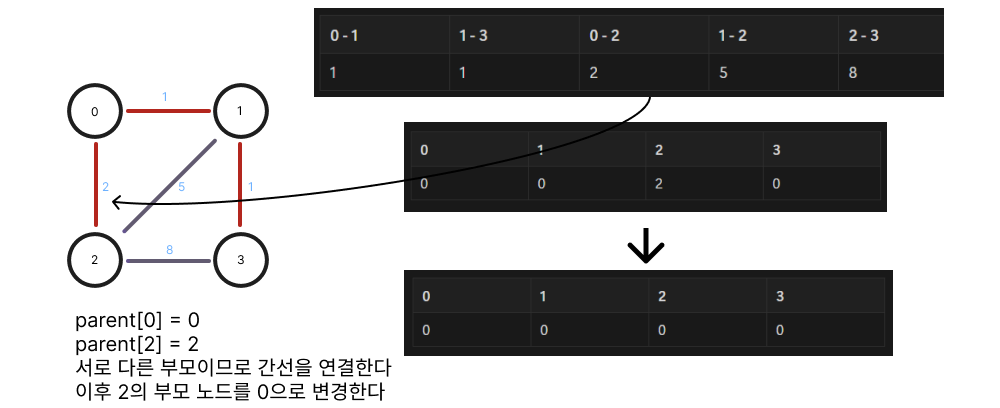

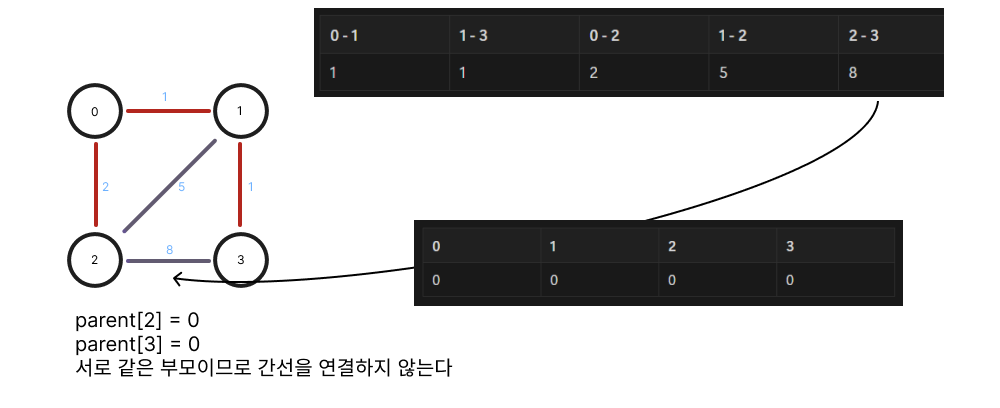
import java.util.*;
class Solution {
private static int[] parent;
private static int find(int x){ // 부모 노드 탐색
if(parent[x] == x)
return x;
return parent[x] = find(parent[x]);
}
private static void union(int x, int y){ // 간선 연결 (부모 노드를 변경)
int root1 = find(x);
int root2 = find(y);
parent[root2] = root1;
}
public int solution(int n, int[][] costs) {
int answer = 0;
Arrays.sort(costs, (o1, o2) -> o1[2] - o2[2]);
parent = new int[n];
for(int i=0; i<n; i++){
parent[i] = i;
}
for(int i=0; i<costs.length; i++){
int node1 = costs[i][0];
int node2 = costs[i][1];
if(find(node1) != find(node2)){ // 부모 노드가 같지 않다면
union(node1, node2);
answer += costs[i][2];
}
}
return answer;
}
}'코딩테스트 > 프로그래머스' 카테고리의 다른 글
| [level 3] 가장 먼 노드 - 49189 (1) | 2024.11.18 |
|---|---|
| [level 3] 아이템 줍기 - 87694 (2) | 2024.11.13 |
| [level 3] 등굣길 - 42898 (0) | 2024.11.12 |
| [level 3] 다단계 칫솔 판매 - 77486 (0) | 2024.11.08 |
| [level 2] 큰 수 만들기 - 42883 (0) | 2024.10.31 |